

Frontline Learning Research Vol.7 No. 1 (2019) 1
- 22
ISSN 2295-3159
aUniversity of Münster, Germany
Article received 13 October 2017 / revised revised 6 September 2018/ accepted 25 October / available online 16 January
Teachers’ beliefs about teaching have been found to affect students’ learning growth. The aim of this study was to investigate effects of teachers’ constructivist and direct-transmissive beliefs on learners’ reading progress and whether these effects are influenced by students’ ability. We measured constructivist and direct-transmissive beliefs of 29 teachers and the progress in reading fluency and reading comprehension of their students (N = 568) at eight points of measurement over one school year. Results of three-level latent growth curve modeling revealed that only teachers’ global, but not reading specific constructivist beliefs, were generally positively related to learners’ progress in reading fluency. Beliefs about teaching had no general effect on growth in reading comprehension, but the relation between constructivist beliefs and students’ progress in reading comprehension was affected by students’ prior skills. Teachers with stronger constructivist beliefs effected higher learning growth for high ability compared to low ability learners within their classrooms. No effects were found for direct-transmissive beliefs. This study adds a more differentiated view to findings concerning the effects of teacher beliefs by showing that effects vary depending on the skill under study (fluency vs. comprehension), and that effects of teacher beliefs may depend on students’ ability.
Keywords: teacher beliefs, beliefs about teaching, reading comprehension, reading fluency
Teachers’ beliefs about teaching have been found to influence teachers’ behaviour and thereby affect student learning (Pajares, 1992; Peterson, Fennema, Carpenter, & Loef, 1989). Two theoretically and empirically distinguishable beliefs about teaching are constructivist and direct-transmissive beliefs. A teacher with high constructivist beliefs for example is convinced that students play an active part in their learning and that they should and will develop their own problem-solving strategies. In contrast, a teacher who holds a direct-transmissive view about teaching believes that a teacher should guide students´ learning process.
Most of the research on teacher beliefs has shown that teachers’ high constructivist and low direct-transmissive beliefs are positively related to higher learning progress (Dubberke, Kunter, McElvany, Brunner, & Baumert, 2008; Peterson et al., 1989; Souvignier & Mokhlesgerami, 2005; Staub & Stern, 2002). Nevertheless, in a sample of particularly low achieving students, contrary results were found (Behrmann & Souvignier, 2013). Thus, similar to the concept of child x instruction interactions (e.g. Connor, Morrison, & Petrella, 2004), which assumes that effects of instruction depend on the fit to students’ abilities, also effects of teachers’ beliefs might vary depending on learners’ initial skills. Therefore, the goals of our study were to contribute to the research on effects of teachers’ beliefs by studying—as yet under-investigated¬—students in primary school in the domain of reading and—more importantly—to investigate whether these effects are influenced by prior abilities of individual students or the respective classroom.
Beliefs are subjective evaluations on whether a specific proposition is true (e.g., Pajares, 1992; Richardson, 2003). They can be distinguished from knowledge, which is rather based on logical argumentation, fact and thus, expert consensus. In contrast, beliefs are non-consensual because they are rather built on personal emotional experiences (Behrmann & Souvignier, 2013; Nespor, 1987; Pajares, 1992; Richardson, 2003). Teachers’ beliefs are assumed to be very important as they affect what happens in the classroom (e.g., Buehl & Beck, 2015; Dubberke et al., 2008; Kagan, 1992; Peterson et al., 1989; Staub & Stern, 2002). They refer to issues that are relevant to teachers’ profession such as their own teaching effectiveness, the nature of knowledge, and how students should be taught (e.g., Pajares, 1992). Hence, beliefs about teaching, in general, cover all aspects of the spectrum on quality of education (Fives, Lacatena, & Gerard, 2015). Within the category of beliefs about teaching, constructivist and direct-transmissive beliefs are most apparent. Case studies using analyses of teacher talk during shared planning time (Gill & Hoffman, 2009) and other qualitative methods mostly revealed constructivist and direct-transmissive beliefs among teachers (see Fives et al., 2015; Kleickmann, 2007). Furthermore, it was demonstrated that operationalisations of constructivist and direct-transmissive beliefs predicted teaching behaviour as well as students’ learning outcomes (e.g., Dubberke et al., 2008; Staub & Stern, 2002).
Constructivist views on learning and teaching can be related to cognitive constructivist learning theories (see Savery & Duffy, 1995). According to this perspective, teachers believe that learners play an active role in the process of studying. The underlying idea of learning is that students actively integrate new information into their existing knowledge. To foster an active and autonomous studying process, the teachers’ task is to provide learners with meaningful learning environments (Staub & Stern, 2002).
In contrast, direct-transmissive views on learning and teaching are related to behavioural-associationist learning theories (see Resnick & Hall, 1998). According to this view, teachers explicitly instruct and guide the students through new contents. Thereby, teachers pre-structure the topics and monitor learners’ progress, which leads to a more passive role of the students in the process of knowledge building (Staub & Stern, 2002).
Teachers’ beliefs affect perception, information processing, judgement, decision making, and the way of teaching (e.g., Buehl & Beck, 2015; Dubberke et al., 2008; Kagan, 1992; Pajares, 1992; Peterson et al., 1989). Hattie (2012) concluded that next to commitment, “teachers’ beliefs (…) are the greatest influence on student achievement over which we have some control” (p. 22). To date, several studies have examined the influence of teachers’ constructivist or direct-transmissive beliefs, showing either positive or negative effects on students’ progress. Nevertheless, the number of such studies is limited.
Peterson et al. (1989) investigated a sample of 39 first-grade math teachers and found constructivist views to be positively related to learners’ mathematical word problem solving. Staub and Stern (2002) surveyed 27 teachers and similarly demonstrated that constructivist beliefs were positively linked to students’ growth in mathematical word problem solving in second and third grade. Studying effects of teachers’ transmissive beliefs in a sample of 155 ninth and tenth-grade school teachers, Dubberke et al. (2008) found a negative relation between strong transmissive beliefs and student achievement in mathematics. In reading, only two studies have been conducted, yet. In line with studies in mathematics, data from Souvignier and Mokhlesgerami (2005) revealed a positive relation between constructivist beliefs and learning growth in reading strategy knowledge for fifth and sixth-grade students from the highest school track. Behrmann and Souvignier (2013) studied a sample of particularly low performing sixth and seventh graders. In contrast to prior research, they found advantages of direct-transmissive beliefs concerning learners’ declarative and procedural reading strategy knowledge but not their reading fluency.
Summing up the findings in the literature, positive relations between teachers’ constructivist beliefs and students’ learning growth have been found in mathematics and reading within groups of average to high performing students, whereas direct-transmissive beliefs seem to be negatively related to student learning. This might be explained by higher cognitive activation and motivational advantages of teaching methods that are in line with constructivist beliefs (e.g., Dubberke et al., 2008; Savery & Duffy, 1995; Staub & Stern, 2002). Nevertheless, the opposite pattern of findings in a sample of particularly low achieving students (Behrmann & Souvignier, 2013) raises the question of whether these effects depend on students’ initial ability. Following the concept of child x instruction interactions, Connor et al. (2004) found that high achieving students benefitted from more self-regulated phases of reading, while lower performing students needed more pre-structured teaching. Given that beliefs affect teachers’ decision-making process and their teaching, the same interactional effects as those between child x instructions might exist for teacher beliefs. Thus, a teacher with high constructivist beliefs who provides much child-managed instruction meets the needs of high but not those of low achieving students. In contrast, a teacher who uses many phases of teacher-managed instruction due to his or her high direct transmissive beliefs, might affect higher growth for the low but not the high achieving students in the classroom.
The short review of studies that analysed the relation between teachers’ beliefs and learning progress reveals that the majority of studies have been conducted in the domain of mathematics. Only two studies (Behrmann & Souvignier, 2013; Souvignier & Mokhlesgerami, 2005) investigated effects of teachers’ beliefs on growth in students’ reading related skills. In these studies, reading achievement was assessed specifically according to reading fluency and knowledge of reading strategies. Effects on reading comprehension, however, have not been studied yet. Therefore, the goal of our study was to broaden the empirical basis concerning effects of teachers’ beliefs in the domain of reading, differentiating between the two key constructs of reading fluency and reading comprehension (National Institute of Child Health and Human Development [NICHD], 2000).
Reading fluency consists of word recognition accuracy and reading speed (Samuels, 1979). It is based on the automation of word recognition (e.g., NICHD, 2000) and therefore relies on large amounts of student-driven decoding practice (Rasinski, Reutzel, Chard, & Linan-Thompson, 2011). Students’ reading fluency increases from grade to grade with a decreasing growth rate over time (Parrila, Aunola, Leskinen, Nurmi, & Kirby, 2005; Tilstra, McMaster, Van den Broek, & Kendeou, 2009).
Reading comprehension in contrast, is a process of constructing a subjective representation of textual information (Kintsch, 1998). Concerning this skill, two sub-processes can be distinguished. One of them results in a local semantic representation of information explicitly inherent to the text. To build this so-called textbase, the reader has to infer meaning from connecting information of words and sentences of smaller units of a text. The other sub-process connects the semantic information of the textbase with prior knowledge to build a meaningful macrostructure representation of the text, which is called situation model. This skill is based on elaboration, organization and metacognitive processes and thus, cannot be automatised. Cromley and Azevedo (2007) showed that background knowledge about the content of a text, strategies and vocabulary are important predictors to knowledge-based inferences as well as to reading comprehension itself. Longitudinal studies revealed mixed results about growth trajectories. Studies of Parrila et al. (2005) as well as of Farnia and Geva (2013) showed that reading comprehension growth decreases over time. Nevertheless, studies of Tilstra et al. (2009) as well as of Nation, Cocksey, Taylor, and Bishop (2010) revealed that growth rates do not decrease over time, but rather follow a linear growth pattern.
From the delineation of these two different reading skills, it becomes obvious that they consist of entirely different cognitive processes. While reading fluency is based on automatised word recognition, reading comprehension is based on prior knowledge, metacognitive processes and consciously made inferences. Consequently, successful instructional designs to support these skills vary concerning the amount of teacher and student guided activities. Reading interventions designed to support reading fluency like Paired Reading (Topping, 1987) and Repeated Reading (Samuels, 1979) encourage students to play an active role in the learning process. These methods especially rely on extended practice so that there is only little need for direct instruction. Reading programs to foster reading comprehension (e.g., Brown & Pressley, 1994; Souvignier & Mokhlesgerami, 2006; Paris, Cross, & Lipson, 1984), however, demand an active role by the teacher who is supposed to directly instruct and model cognitive and meta-cognitive strategies for reading by a relatively large part. Thus, teacher guided instruction may be necessary especially for lower performing students to successfully develop their reading comprehension.
From a learning theory perspective, constructivist and direct-transmissive beliefs are contradictory (Behrmann & Souvignier, 2013; OECD, 2009; Staub & Stern, 2002). Thus, the assessment of beliefs has often been conceptualized on a constructivist-transmissive continuum, using only one single scale (e.g., Peterson et al., 1989; Souvignier & Mokhlesgerami, 2005; Staub & Stern, 2002). Dubberke et al. (2008), however, used one scale to assess direct-transmissive beliefs only. Likewise, Behrmann and Souvignier (2013) used separate constructivist and direct-transmissive scales in addition to a constructivist-transmissive continuum scale. This alternative approach follows the argumentation that teachers may hold even potentially contradictive perspectives on effective teaching (see Fives et al., 2015). It was found that teachers can endorse constructivist and direct-transmissive views at the same time (Organisation for Economic Co-operation and Development [OECD], 2009; Fives et al., 2015; Snider & Roehl, 2007). Teachers’ beliefs about teaching may be inconsistent because of a vast range of different teaching situations that teachers have to face and to consider (Behrmann & Souvignier, 2013; Fives et al., 2015). This is supported by means of factor analytical results, which show that constructivist as well as direct-transmissive beliefs each build their own factors (e.g., Bunting, 1985; Woolley, Benjamin, & Woolley, 2004). Thus, conceptualizing and measuring constructivist and direct-transmissive views on teaching with separate scales may be more appropriate (Behrmann & Souvignier, 2013; Buehl & Beck, 2015; Woolley et al., 2004). Nevertheless, strong negative correlations between measures of constructivist and direct-transmissive scales indicate that teachers generally tend to favour one of the two orientations (see Behrmann & Souvignier, 2013).
Another important aspect of beliefs about teaching is their specificity with respect to a certain content. Beliefs can be conceptualized as content specific (i.e. related to reading instruction) as well as content general. Content specific beliefs about teaching may be especially important because they may more precisely apply to content specific teaching situations (Peterson et al. 1989; Staub & Stern, 2002). Reading specific beliefs may thus, especially affect students’ reading competence growth. Nevertheless, global beliefs about teaching may also have an important impact on students’ learning of reading skills because they may affect teaching on a more general level in most teaching situations. Given that reading is not limited to a specific subject like maths, it seems reasonable to assess teachers’ beliefs both in a content specific and in a content general way.
To analyse the effects of teachers’ beliefs on learners’ progress, usually data from longitudinal designs with pre- and posttests on student achievement have been used. Difference scores from two measures as an indicator for learning progress, however, have been criticized with respect to limited reliability (Willett, 1989). Assessing change with multiple points of measurement creates advantages over pre-post measures, because it boosts the reliability of the growth rate estimates (e.g., Singer & Willett, 2003; Willett, 1989). Willett (1989) demonstrated that every additional point of assessment helps to deflate standard errors and concluded that “with sufficient waves added, the influence of fallible measurement rapidly dwindles to zero” (p. 598). Furthermore, Speer and Greenbaum (1995) demonstrated that growth modeling based on multiple points of assessment is more sensitive to change than methods based on pre-post measures. In this study, we enhance the reliability of the assessment of growth by modeling learning progress across eight points of measurement over one school year.
Our study addressed three research questions:
First, we were interested in general effects of teachers’ beliefs on students’ progress in reading. Consistent with previous studies, we expected positive effects from constructivist beliefs and negative effects for direct-transmissive views on reading fluency and comprehension.
Second, we wanted to investigate if students’ initial achievement moderates the effects of teachers’ beliefs on students’ reading progress. Given the different findings in reading with positive effects of either constructivist or direct-transmissive beliefs for high and low achieving students, respectively, we anticipated that constructivist beliefs might be supportive for students with higher reading skills, whereas direct-transmissive beliefs might be more suitable for students with lower reading skills.
Third, given that moderating effects might not only become apparent at the individual level but also in the entire classroom, we also studied whether effects of teachers’ beliefs on classrooms’ reading growth were moderated by the average prior ability of the classroom. In concordance with the second hypothesis, we expected that constructivist beliefs are supportive for classrooms with higher initial reading ability and direct-transmissive beliefs to be more helpful for classrooms with lower initial reading ability. Regarding each of the hypotheses, we expected the same effects for growth in reading fluency and reading comprehension.
Teachers from a previous reading intervention study who voluntarily decided to implement learning progress assessment in the school year 2012-13 were asked to participate in this study. Out of 47 teachers, 29 teachers (83% female) agreed to participate. On average they were about 48 years old (M = 47.90 years, SD = 10.99) and had a teaching experience of approximately 22 years (M = 22.45 years, SD = 12.05). The student sample consisted of 568 fourth graders (49% female; 17% with a migration background) from 29 classrooms in 18 German schools. At the first point of measurement, students were approximately 10 years old (M = 9.73 years, SD = 0.48). Teachers’ beliefs were assessed with a questionnaire at the beginning of the school year before repeatedly assessing students’ reading skills. Participation was voluntary. Neither teachers, nor students received incentives for participation.
2.2.1 Teacher beliefs
Following the procedure by Behrmann and Souvignier (2013), teachers rated their beliefs on three different scales. The constructivist orientation scale (COS) measures constructivist beliefs with regard to reading instruction. An example for an item of the COS is: “In order to learn how to competently handle texts, it is helpful to let students discuss their own text approaches.” Internal consistency of this scale was acceptable (Cronbach’s α = .75). The global orientation scale (GOS) quantifies global constructivist beliefs. An example for an item of the GOS is: “Curricular activities should primarily focus on students’ practical learning experiences.” Internal consistency of this scale was also acceptable (Cronbach’s α = .72). The direct-transmissive orientation scale (DOS) measures direct-transmissive beliefs specifically referring to reading instruction. An example for an item of the DOS is: “Most students are unable to discover reading strategies on their own, and therefore need explicit instruction.” For this scale, internal consistency proved to be good with Cronbach’s α = .82. The COS, GOS, and DOS measures consist of six items each with a four-point Likert scale, ranging from (1) I strongly disagree to (4) I strongly agree (see Behrmann & Souvignier, 2013). A content general direct-transmissive scale was not provided by Behrmann and Souvignier (2013) and thus not used in this study.
2.2.2 Reading progress
Students’ progress in reading fluency and reading comprehension was assessed over one school year using an internet-based tool for learning progress assessment (see Förster & Souvignier, 2014). At intervals of three weeks, students individually completed one of eight equivalent reading tests during self-study periods at school. Each test took about 10 min on average.
In each of the eight tests, learners first completed a maze task in which every seventh word of a text was deleted. Students were instructed to replace the 24 gaps as quickly as possible by choosing the correct word among three choices. No time limit was given to assure that all learners had read the complete text. In addition to the number of correct replacements, we also recorded the time needed to complete the maze task. Given the need to simultaneously recognize words and construct meaning from text to select the gaps, this test format is in accordance with definitions of reading fluency (e.g., Samuels, 1979). We measured reading fluency in the current study as the number of correctly selected words within 1 min.
After completing the maze task, students answered 16 comprehension questions that referred to the text from the maze. While answering the questions, the complete and correct text was visible. Learners were required to choose the correct answer from four choices. Following models of text comprehension (e.g., Kintsch, 1998), half of the questions addressed text-based information and thus asked for information that was explicitly contained in the text. The other eight questions assessed the construction of a situation model by requiring students to make inferences from the given information. No time constraints were given to complete the task. We used the number of correct answers as the reading comprehension measure.
Eight tests were applied over the whole assessment period. Four of the tests were based on non-fictional texts about animals and the other four texts were based on fictional detective stories. Fictional and non-fictional texts were performed alternately.
Prior research has documented the psychometric quality of the reading tests (see Souvignier, Förster, & Salaschek, 2014). Internal consistencies were found to be high with Cronbach’s α ranging from .86 to .89. In addition, correlations to standardized paper-pencil tests measuring reading fluency (r = .60 to .66) and reading comprehension (r = .63 to .65) revealed satisfying criterion validity. The tests demonstrated that they are sensitive to student improvement with significant reading growth over the eight points of measurement.
We removed outliers that were two standard deviations below the average of an individuals’ points of measurement because of selective distortion of the data due to guessing, inattention, or failure to make a decision. We also removed outliers that were two standard deviations above the individual average on reading fluency, because fast guesses likely increased these measures. In total, 1.6% of the data were excluded for reading fluency and 0.7% for reading comprehension. Data coverage at any point of measurement was continuously higher than 90% with the highest rates of data coverage at the last point of measurement. In total, 6.6% of the reading fluency and 4.4% of the reading comprehension values were missing. We used Full Information Maximum Likelihood (FIML) to account for missing data, which has shown to be particularly useful for structural equation modeling (Enders & Bandalos, 2001). With this procedure, all existing data are used to estimate model parameters.
Data were nested in three levels. Points of measurement (level 1) were nested in students (level 2) which were nested in classrooms (level 3). Thus, we applied a three-level latent growth curve model using Mplus 8 (Muthén & Muthén, 2017). With this analysis, prior competence can be modeled on the level of individual students as well as on the level of classrooms. Thereby we accounted for the nested structure of the data and prevented underestimation of standard errors (Bryk & Raudenbush, 1988).
Given that linear and non-linear reading growth rates have been reported in the literature (Parrila et al., 2005; Tilstra et al., 2009), we considered linear, quadratic, and free-loading models for the most suitable curve estimation of our data (Bollen & Curran, 2006; Duncan, Duncan, & Strycker, 2006). We rejected the free-loading model, because its growth factor can only be interpreted as a measure for progress when the determined shape is close to linearity (Duncan et al., 2006). After scrutinizing the mean scores of the eight measurement points (see Table 4), we only compared fit indices between linear and quadratic models. A linear growth factor is the most legitimate measure of progress for these models (see Bollen & Curran, 2006). Compared to a linear model, a quadratic model additionally has a quadratic growth factor, which is an indicator for an acceleration or deceleration trend in growth over time. Its linear factor thereby represents the growth rate at the first measurement point (Bollen & Curran, 2006). To specify a quadratic model with a comparative linear measure of learning progress over the whole period of the study, we fixed the variance of the quadratic growth factors to zero at the individual and classroom levels. Thus, the acceleration or deceleration trend in growth over time was constrained to be equal across all classrooms. At the individual student level, the quadratic factor mean is zero, because lower level (i.e. student level) scores are deviations from means of higher levels (i.e. classroom level) in multilevel modeling. With no variation and a mean of zero, the quadratic growth factor on the individual level remained unspecified. This resulted in a quadratic model with linear growth factors at the individual and classroom level, which could be used as comparable measures of growth over the whole period of measurement.
Next, solutions of the above described linear and quadratic growth models were compared by using Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). Fit indices for reading fluency and reading comprehension suggested an advantage for the quadratic model (see Table 1). The classroom level quadratic factor was negative for reading fluency (p < .001) and for reading comprehension (p < .001) indicating decelerated growth over time. Based on this result, the quadratic model was selected for the reading fluency and comprehension data.
Table 1
Fit indices of linear and quadratic three-level latent growth curve models without covariates

Teachers’ beliefs and the interactions of teachers’ beliefs with prior abilities on student and class level were stepwise included into a baseline model resulting in three additional models. All models are shown in Table 2 and coefficients are described in Table 3. Given the three different measures of teachers’ beliefs and the two reading outcomes, we ran 18 models in total.
Teacher belief data were centred at the grand mean before they were added as covariates to the baseline model in a stepwise procedure (Models 1-3, Table 6 & 7). This procedure allows for unbiased estimates of higher-level interaction effects (Enders & Tofighi, 2007).
In Model 1, only a test for a main effect of teachers’ beliefs on the classrooms’ average learning progress (γ101) was conducted by including the third-level predictor teacher belief (tbj). Model 2 additionally tested a cross-level interaction effect (γ201) to analyse if students’ initial achievement moderates effects of teachers’ beliefs on students’ learning gains. Thereby, students’ initial reading achievement (r0ij) and progress (r1ij) are determined in relation to their own classrooms’ average initial achievement (ß00j) and progress (ß10j). To determine the cross-level interaction effect in this way, a random effect of prior skill levels on learning growth was required for the student level (ß11j). Thus, a regression of individual deviations from class level learning growth (r1ij) on individual deviations from class level prior ability levels (r0ij) was modelled. The parameters r0ij and r1ij thereby indicate the group mean centred individual deviations from the classrooms prior ability and learning progress, respectively. Having group mean centred lower level predictors (as r0ij in our case) is crucial to estimate cross-level interaction effects because then, estimates are not biased by interaction, which may be potentially present on class level (Enders & Tofighi, 2007). Model 3 furthermore tested if the classrooms’ initial skills moderated the effect of teachers’ beliefs on the classrooms’ learning growth (γ103). In addition, a test for effects of initial competences on learning progress at the classroom level (γ102) was added to Model 3 to allow unbiased estimations of the classroom level interaction effect.
Table 2
Overview of the three-level latent growth curve models

Table 3
Description of Coefficients of Model 3
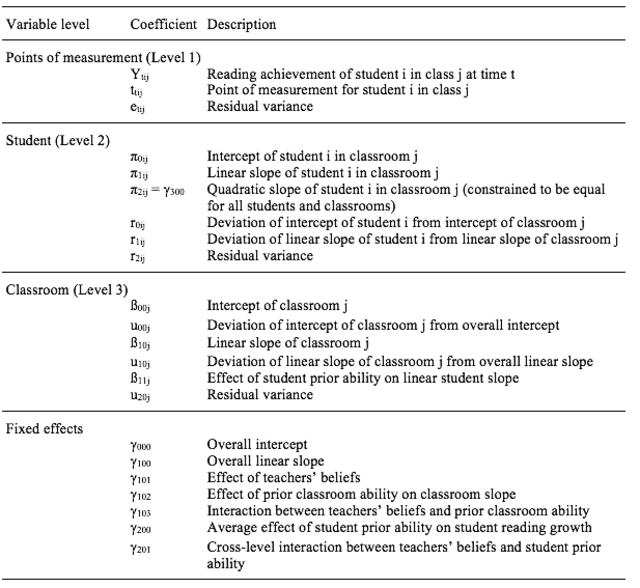
Table 4 shows the means, standard deviations, and intercorrelations of reading fluency and reading comprehension data at all points of measurement. All measures of reading ability were highly correlated.
Table 5 presents the descriptive statistics of the belief scales. Moderate to strong positive and negative correlations were found between the COS, GOS, and DOS measures as expected. A mean score of M = 3.36 for the COS and M = 3.53 for the GOS on a 1 to 4 scale indicated that teachers on average agreed with the reading specific and global statements of the constructivist orientation scales. The mean score for the DOS was in the middle of the scale (M = 2.48).
Table 4
Intercorrelations, means, and standard deviations of reading fluency and reading comprehension at eight points of measurement (N = 568)
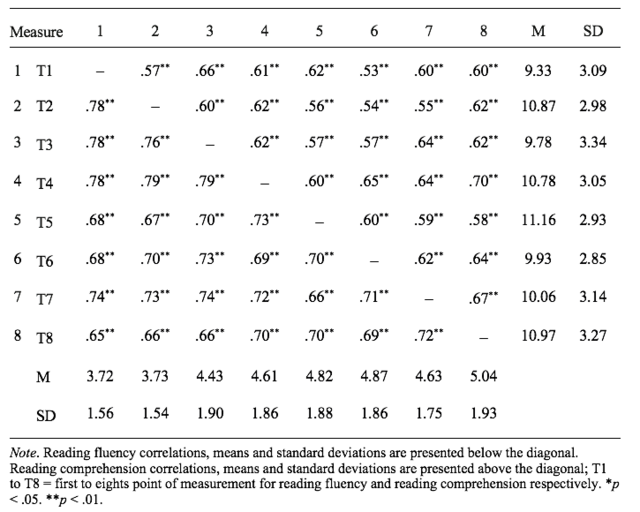
Table 5
Intercorrelations, means, standard deviations of the COS (N = 29), GOS (N = 29) and DOS (N = 29) scales

As shown in Table 6, the quadratic three-level latent growth curve model for reading fluency without covariates revealed that students reached an average of 3.63 correctly selected gaps per min at the beginning of fourth grade (γ000). The linear growth (γ100) was 0.39 gaps every three weeks with a moderate deceleration trend indicated by a negative quadratic factor (γ300 = -0.03). We found substantial within-class variance in students’ reading fluency at the beginning of the school year (r0ij = 1.93, p <.01) but no significant variation in linear growth over the course of the school year (r1ij = 0.01, p = 0.15). The same pattern was observed at the classroom level. Initial abilities significantly differed between classrooms (u00j = 0.13, p < 0.01), whereas linear growth in reading fluency did not differ between classrooms (u10j = 0.002, p = 0.17).
Students answered on average 9.79 questions correctly on the reading comprehension test (γ000) at the beginning of fourth grade (see Table 5) and had a linear improvement rate of 0.30 answers (γ100) every three weeks on average with a moderate deceleration trend indicated by a negative quadratic factor (γ300 = -0.03). Similar to the results found for reading fluency, reading comprehension significantly differed between students from the same classroom at the beginning of the school year (r0ij = 4.91, p <.01), but variation in linear learning growth between individual students of the same classroom was not significant (r1ij = 0.004, p = 0.66). The opposite pattern was found at the classroom level. Although no significant differences were found for prior reading comprehension (u00j = 0.66, p = 0.11), different classrooms showed different linear growth in reading comprehension over the school year (u10j = 0.01, p <.01). Despite finding some non-significant variances at the student and classroom levels, we analysed the effects of teachers’ beliefs, because adding beliefs as covariates may increase testing power by reducing error variance in the dependent variable (Aberson, 2010).
Table 6
Parameters for the three-level latent growth curve baseline models for reading fluency and reading comprehension

Results of the three-level latent growth curve models revealed that teachers’ global constructivist beliefs were positively related to students’ progress in reading fluency (see Table 7, Model 1 & 2) . No significant effects were found for the reading specific COS scale and direct-transmissive beliefs on reading fluency growth. The results for reading comprehension showed that none of the teacher belief scales was significantly related to students’ learning growth (see Table 8, Model 1 & 2).
Table 7
Effects of teacher beliefs on progress in reading fluency
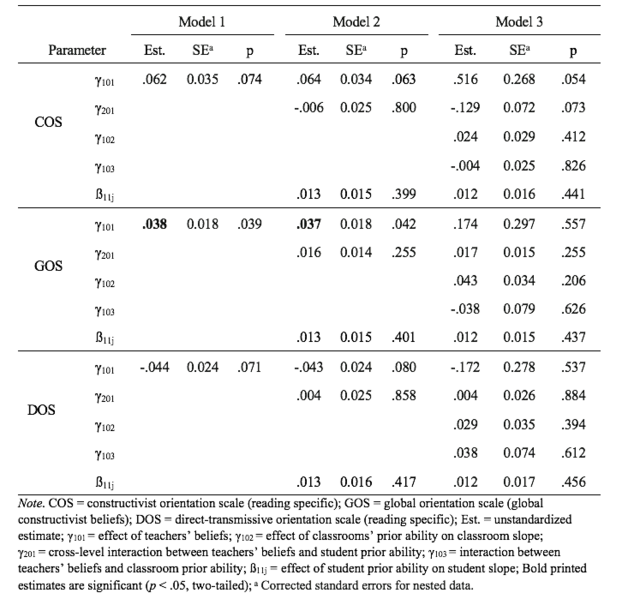
We also analysed whether students’ prior ability (relative to the average classroom ability) moderated the effects of teachers’ beliefs on students’ deviation from the average growth of the classroom. Results for reading fluency indicate that students’ initial skills did not affect the relation between teachers’ beliefs and individual learning growth (see Table 7, Model 2 & 3). As hypothesized, however, a significant cross-level interaction was found for reading comprehension (see Table 8, Model 2 & 3). The effect of teachers’ constructivist beliefs on students’ reading growth was positively moderated by students’ prior skills. Hence, teachers with higher constructivist beliefs affected higher growth in reading for students with higher prior ability compared to students with lower ability within their classrooms. We found no interaction for direct-transmissive beliefs (see Table 8, Model 2 & 3).
Table 8
Effects of teacher beliefs on progress in reading comprehension
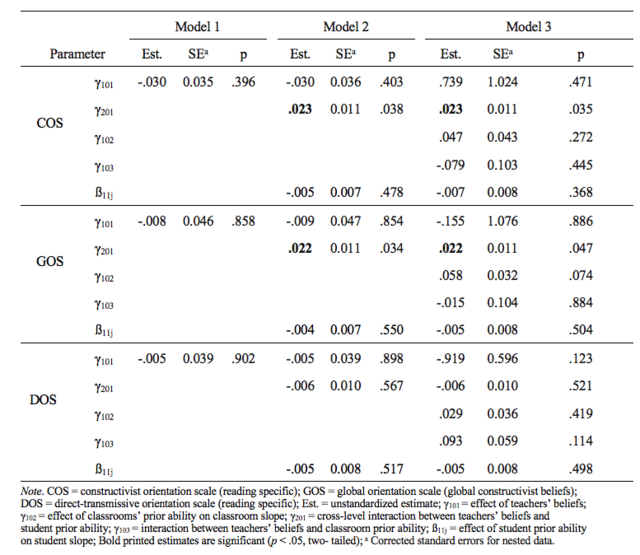
We additionally tested whether the prior average reading skills of the classroom moderated the effect of teachers’ beliefs on growth in reading fluency and reading comprehension on the classrooms level. The results show that the classrooms’ prior competences did not moderate the effect of teachers’ beliefs on classrooms’ learning progress (see Table 7 & 8, Model 3, respectively). In addition, classrooms’ initial reading fluency and reading comprehension ability had no general effect on learning.
In this study, we used multilevel latent growth curve modeling to investigate effects of teachers’ constructivist and direct-transmissive beliefs on students’ progress in reading fluency and reading comprehension. Moreover, we examined whether effects of teachers’ beliefs depended on prior reading ability. We found that teachers’ global constructivist beliefs had a general positive effect on students’ reading fluency but not on their reading comprehension progress. No significant relations were found between reading specific constructivist beliefs or direct-transmissive beliefs and student growth in reading fluency and reading comprehension. As hypothesized, we found an interaction of teacher beliefs and prior abilities. High achieving students in contrast to low achieving students benefited in their reading comprehension growth from a teacher who holds high constructivist beliefs. The positive effect of teachers’ global constructivist beliefs on reading fluency was unaffected by prior abilities. Thus, effects of teacher beliefs seem to depend on the skill under study and interact with students’ prior ability, which we discuss in the following section.
Our finding that general constructivist beliefs of teachers were positively related to students’ growth in reading fluency is in line with our hypotheses. The same effect, however, was expected but not found for reading comprehension and no main effects of reading specific teacher beliefs were found. Also, whether or not prior abilities moderated effects of teacher beliefs seems to depend on the respective skill. So how can we explain this pattern of results? Given the different findings for reading fluency and reading comprehension, one starting point is to reflect on the specific reading skills and effective ways of teaching these skills. While reading fluency is characterized by the automation of word recognition, reading comprehension requires to intentionally apply reading strategies to construct a representation of the situation model and to connect new information to prior knowledge. Consequently, effective reading fluency instruction aims to automatize word recognition, for example by instructing students to (repeatedly) read text passages aloud (e.g., repeated or paired reading; Topping, 2006). These decoding practices are mainly student-driven without a particular need of teacher instruction and thus easily match with high constructivist beliefs. Effective instruction of reading comprehension, in contrast, is characterized by the explicit instruction of reading strategies by the teacher (Souvignier & Mokhlesgerami, 2006). This contradicts constructivist views of teaching after which students should and will develop their own problem-solving strategies. Actually, as indicated by our finding that prior student ability moderated effects of global and specific constructivist beliefs on students’ progress in reading comprehension, it seems that high achieving students indeed tend to develop their own effective reading strategies and thus profit when a teacher with high constructivist beliefs teaches them. Low achieving students, however, might be overstrained to self-regulate their reading comprehension without explicit instruction of strategies. Following this argumentation, we would expect that teachers with high constructivist beliefs positively affect the development of skills that require student-driven practices to automatize processes (e.g. word recognition or basic mathematical skills) for all students independent of their prior ability. If, however, the skill is not characterized by high automation but requires strategic behaviour, teachers who provide much student-managed but less teacher-managed instruction due to their high constructivist beliefs might positively affect learning for the high but not the low achieving students. This assumption is in line with findings on child x instruction interactions by Connor and colleagues, who showed that low achieving students benefit from teacher-managed instruction but high achieving students benefit from child-managed instruction (e.g. Connor et al., 2011; 2004).
The positive effects of high constructivist beliefs on student learning have been ascribed to higher cognitive activation and motivational advantages of teaching methods used by teachers with high constructivist beliefs (e.g., Savery & Duffy, 1995; Staub & Stern, 2002). These positive motivational advantages, however, will likely not occur if students feel overstrained by the task. We assume that the teaching methods of teachers with high constructivist beliefs will probably be more child-managed and less teacher-managed, and that those methods will likely overstrain low achieving students, who need explicit guidance to build up self-regulated strategic reading behaviour. Regarding reading fluency, in contrast, most fourth-grade students will be able to cope with the task of just reading a text, which might enhance their automation of word recognition but not their ability to understand texts. This would explain why we find general positive effects of constructivist beliefs on growth in reading fluency but not in reading comprehension. Reading specific views about teaching had no effects on learning growth, which is in contrast to our hypotheses as well as to findings showing that content specific constructivist beliefs about teaching can effect students’ learning (e.g., Staub & Stern, 2002; Souvignier & Mokhlesgerami, 2005). Nevertheless, results point to expected directions. Effects of reading specific beliefs on learning growth may be weaker, because compared to global beliefs, they may be rather limited to lessons specifically dedicated to foster reading skills.
We found no effects for direct-transmissive beliefs. Thus, although variance in direct transmissive beliefs was highest, this variance did not explain differences in reading fluency or reading comprehension growth. Most prior studies have assessed teacher beliefs using a single continuum. The only study investigating teacher beliefs on separate scales in reading is very specific as the teachers applied a strategy-based reading program (Text Detectives; Behrmann & Souvignier, 2013). This pattern of results suggests that differences in direct-transmissive beliefs in contrast to constructivist beliefs might be less influential on teaching behaviour and thus do not explain differences in student learning.
Finally, it should be noted that the interactions with prior ability were found on the student but not the classroom level. An explanation may be that significant variance in prior abilities was found between students of the same classrooms, while the average reading skills of the classrooms in this study seemed to be similar (see Table 6).
A limitation of this study is the small variance in student and classroom level reading growth, despite the representative range of classrooms. The limited variation between classrooms’ growth in reading may have masked effects of teacher beliefs. Investigating interaction effects in a sample with a higher variance within and between classrooms would be desirable.
Moreover, when interpreting our results, one should consider that the belief measures might be affected by social desirability regarding constructivist beliefs leading to ceiling effects and low variances in the COS and GOS scales. Assuming that social desirability affected our measures it is likely that effects of teachers’ beliefs on students’ reading growth were rather masked than increased by potentially inflated standard errors. Given that standard errors are similar for effects of constructivist and direct-transmissive beliefs (see Tables 7 & 8), however, we assume that the impact of social desirability may be rather negligible.
Unfortunately, the construct validity of the three belief scales could not be confirmed using confirmatory factor analysis due to the limited teacher sample. Nevertheless, the moderate to strong correlations between the three scales indicate that they are partly independent of each other.
In the introduction, we stated that content general as well as reading specific beliefs about teaching are relevant. Nevertheless, similar to the study conducted by Behrmann and Souvgnier (2013), our study included a global constructivist, but not a global direct-transmissive belief scale. Further studies should investigate effects of both global constructivist and direct-transmissive beliefs to fully discriminate between content-specific and global beliefs.
Analysing effects of teachers’ beliefs on students’ learning is largely based on the assumption that beliefs and classroom behaviour of teachers are closely connected (e.g., Buehl & Beck, 2015). In research designs without classroom observations, as in our study, the variability of teachers’ instructional activity remains an open issue. Conversely, by not observing teacher behaviour we ensured unimpaired business-as-usual instruction and thus high ecological validity of the study.
Regarding the external validity of this study, it should be considered that the results and conclusions of this paper are based on reading skill data from a sample of fourth grade classrooms only. Consequently, generalization about different grades and content is limited, especially as our results indicate that effects of teachers’ beliefs may depend on the specific skill under study.
The teachers of this study had access to the results of their students’ reading tests, which is a feature of the learning progress assessment tool (Förster & Souvignier, 2014). Thus, in addition to their personal impressions, they had another objective information about the development of their students. We do not assume that the availability of more student information alone is responsible for the effects. Moreover, quantity and quality of additional information was the same for all teachers. Given that effects of both teacher beliefs and learning progress assessments are assumed to be mediated by instructional behaviour, future studies should investigate the interplay of teacher beliefs, learning progress assessment and instructional behaviour. For example, according to constructivist views, prior knowledge is considered to be particularly important for the learning process (Savery & Duffy, 1995; Staub & Stern, 2002). Thus, teachers with high constructivist views might be more receptive to additional assessment information.
Our study complements existing research in a number of ways. First, we investigated effects of teacher beliefs in the domain of reading and–up to our knowledge–provide the first results for effects on reading comprehension. Second, we analysed under which conditions which teacher beliefs positively affect students’ reading progress. The analysis of interactions between student ability and different teacher beliefs on both student and classroom level adds to our knowledge of the interplay between teacher and student variables during the learning process and provides a novel perspective to child x instruction interactions. Third, we assessed reading fluency and reading comprehension progress with eight measurements across the school year, thereby ensuring the reliable assessment of student progress.
This work partly confirmed general effects of teachers’ beliefs about teaching. Global constructivist, but not reading specific beliefs about teaching had an impact on students’ reading fluency. No general effects of teachers’ beliefs on reading comprehension progress were found but teachers with stronger constructivist beliefs affected higher learning growth in reading comprehension for students with higher prior ability compared to lower performing students within the classrooms. A similar interaction was not found for reading fluency indicating that effects of teachers’ beliefs on growth in reading fluency is unaffected by prior skills. These skill-specific findings for effects of teachers’ beliefs and their interaction with students’ ability might be explained by differences regarding the optimal instruction of these skills that correspond more or less to constructivist views of teaching. Our study thus adds to our understanding of the conditions under which constructivist teacher beliefs are positively associated with student learning.