

Frontline Learning Research Vol.5 No. 1 (2017) 43
- 57
ISSN 2295-3159
aSimon Fraser University, Canada
Article received 27 November / revised 30 September / accepted 26 October / available online 15 February
This paper proposes a philosophical approach to the mathematical engagement involving students and a digital tool. This philosophical proposal aligns with other theories of learning that have been implemented in mathematics education but rearticulates some metaphors so as to promote insight and ideas to further support continued investigations into the learning of mathematics. In particular, this philosophical proposal takes seriously the notion that a priori to activity, there are no objects which in turn challenge the notions of intention, affordance and/or representation. To exemplify this perspective, two episodes of grade nine students using a dynamic geometry software are analysed to elaborate how mathematics can be seen to emerge from working with a tool.
Keywords: post-humanism; materialism; mathematics education; theories of learning
With the proliferation of digital tools in the modern age, the implementation of these tools into the mathematics classrooms is becoming ubiquitous. These tools that include graphing calculators, iPads, iPhones are implemented for the purpose of improving mathematical learning. Since technology is changing so fast and new applications are being created everyday, different learning theories are necessary to accommodate or adapt to these new technologies. Indeed, it is ultimately a philosophical question as to how a material object, a technological/mathematical tool for example, can become part of, contribute to, and help develop mathematical thinking. However, in addressing this philosophical challenge, this paper moves away from the “learner” as central and asserts that mathematics emerges amid the dynamic relations of humans and materials. The highlighting of materials partially aligns with Actor Network theorists since Actor Network scholars value the contributions of material objects in the production of knowledge. However, this study notes that materials are variable and often boundary-less and as such the perspective taken in this paper takes seriously the positioning exemplified by Ingold’s (2011) provocation that there are no materials a priori to an activity.
This paper explores a profound philosophical shift in terms of where it locates the "thinking" in a mathematical activity. This shift has been called post-humanist (Barad, 2007) as well as new materialist (de Freitas & Sinclair, 2014). It is common in teaching to describe knowing in a concrete and human-centric way. “She knows the quadratic formula” is a simple phrase that conveys the ownership of a proposition. However the implication in such statements place the human as central knower and agent. In education studies, the student is often central, and although this seems appropriate within an educational system with a mandate to educate the individual, new theories are pointing to alternate conceptions that may offer productive new ways of understanding tool-based mathematical activity. I adopt the term post-humanist (Barad, 2007) to challenge the isolating tendency or reductionist approach to see the human as the central actor. In post-humanist practice, the human is considered to be just one of many “actors” involved in that practice. Other actors can include such things as tools, social influences, concepts or even a task itself. I draw on post-humanism not to deny the intangible, experiential aspect of mathematical practice but instead to implicate the dynamic and significant effect of the artefact on practice, and, in this study, how this implicates the emergence of the mathematical. That is, the material aspect of working with concrete tools is more than a matter of mastering a tool to exploit its affordances. A student and a tool might instead be seen as being on more equal footing, so that the tool is not simply subjugated to the all-knowing or all-deciding human. In this way post-humanism refers to the idea that mind and matter are not ontologically distinct.
New materialism aligns with the ontological monism of Spinoza and the historical materialism of Marx, adopting the important aspects of the political, the ontological and the epistemological into mathematics education. The term “new”, however, in “new materialism” moves into a world of agency and animation and argues for mobility and action as necessary components to generative development. When distinctions of human agency and matter are challenged, particularly in education, different ways of seeing emerge in how the use of tools can generate interesting ways of thinking about learning. Indeed, similar to learning theories, many current methods privilege the human actor (e.g. in transcripts, in modes of describing events in terms of being actor-driven).
While there are numerous contributory frameworks that address the questions that emerge in an analysis of the relational engagement of a human working with a material, I suggest this study differs from many approaches by adopting both a post-humanist and a new materialist perspective. Throughout this paper I draw on how these perspectives come together in one framing. In part, the post-humanism draws attention away from human and the new materialist approach looks more to the material. It is the combination of both approaches that I suggest differs from previous work in mathematics education.
I suggest that to create turbulence in how one “reads” common learning situations is the first step towards new ways of seeing. I do not present insights based on the intrinsic nature of learning but rather a metaphoric re-description (Hess, 1980) that in and of itself can lead to different ways of seeing. The question addressed in this paper is not about informing educators about the way things are. The purpose of introducing a post-humanist and new materialist approach is for the production of potential possibilities and to explore alternative ways of understanding different framings of mathematical activity. Following from this re-conception of mathematical practice, the underlying question that emerges in this paper asks what insightful understandings and interventions emerge from a post-humanist/new materialist approach.
In the first section, I discuss current approaches to theorizing tool-use in mathematics education. I then contrast these with a post-humanist, new materialist perspective on tool-use, which challenges the human-centric view of activity and argues for a process ontology. I draw upon the work of Andrew Pickering and articulate his resistance/accommodation model as the way in which scientists and mathematicians create new machines and/or ideas. I also expand on Tim Ingold’s work and his argument that tools are not distinct entities and should be seen as narratives—that is, how they may contribute to function. In this study I present two narratives that support a storied knowledge of actual engagement . Finally, I briefly describe the work of Karen Barad, who offers the powerful notion of intra-action in her new materialist account of the nature of scientific concepts, in which concepts and tools, for example, are seen as a single entity (a relation) rather than as two interacting things (or relata). I suggest that each of these scholars has identified particular and distinctive approaches to tools that are relevant to the study of tool-use in the mathematics classroom. I finish with the analysis of two episodes of grade nine students using a dynamic geometry software in terms of the framework described in this paper.
The theoretical foundation of tool-use in mathematics education continues to be problematic (Waltz, 2006). At one extreme, mathematics is valued as a mental discipline where concrete tools are dismissed as being a mere aid to learning, but not as constitutive of the knowing or of the mathematics (see Balacheff, 1988). Another approach is that tools can be considered an essential element to mathematical practice—a position that Rotman (2008) encapsulates nicely when he says that mathematics has been, and will continue to be, involved in a two-way, co-evolutionary relationship with machines. Here, the implication is that there would be no mathematics without mathematical tools, and vice versa.
In mathematics education research, some of the more common frameworks for addressing the challenges of accounting for how tools are brought into and included in mathematical activity are instrumental genesis and semiotic mediation. For example, instrumental genesis suggests the instrumentalizing of an artefact develops over time as people use them for particular purposes, thus transforming them into tools. This approach distinguishes the instrumetalization of a tool as part artefact, part cognitive schema (Artigue, 2002). The individual’s mental schemes together with the artefact’s inherent potential is what makes the artefact an instrument. The artefact is a material object, but an instrument is a psychological construct. Verilon and Rabardel (1995) define this process as one of appropriation, of making the tool one’s own. Instrumental genesis does not focus solely on individuals with tools; instead, it also incorporates socio-cultural issues, including institutional meaning, class norms, and teacher’s expectations. According to Ruthven (2002), these social factors are integral to the activity of instrumentation.
Another well-developed framework for thinking about tools within mathematics education is that of semiotic mediation (Bartolini-Bussi & Mariotti, 2008). The theory of semiotic mediation has been developed specifically within the field of mathematics education with a focus on analysing the semiotic potential of a tool—that is, its potential for linking personal meanings with mathematical ones—and then studying how it can be realized by teachers in classroom interactions. This theory is based on the work of Vygotsky and has been significant in socio-cultural and –historical understanding of thinking.
In each of these frameworks, the tool plays an important role and influences the material situation of learning. Another framework that has recently emerged is proposed by Nemirovsky et al. (2013). Nemirovsky et al. argue against the dualism of tool-mediated expression and mathematical understanding (and its related dualism of body and mind). In their non-dualist approach, they offer an approach to mathematical thinking that involves the temporal and developing entwining of perception and motor skills, and call the “interpenetration” of perception and motor skills “fluency”, the development of which constitutes mathematical thinking. A mathematical instrument for Nemirovsky et al. is material, semiotic and has a set of embodied practices. They contrast their use of the term “instrument” with that of the theory of instrumental genesis, where an instrument is a mixed entity, part artifact (material) and part schema (mental). They see mathematical thinking as the bodily experience of developing fluency on the mathematical instrument, stating, “mathematical activity is constituted by bodily activity” and, correspondingly, mathematical learning as the “transformations in learners’ engagement in mathematical practices” (p. 376).
The theory of enactivism based on systems theory (eg. Varela, Thompson, & Rosch, 1991) has also been implemented in mathematics education and goes further in challenging boundaries of human body and environment. Goodchild (2014) describes enactivism “as active processes that occur directly through the interaction between the cognizing subject and the environment, rather than as a construction of representations of the environment by the cognizing subject” (page 210).
These theories have contributed insightful approaches and encourage further exploration to enrich perspectives and provide continued generative ways of thinking about education. The approach outlined in this paper aligns in many way with the previously mentioned frameworks. I suggest however that this study deviates from these approaches in two significant ways. I draw upon Ingold’s notion that there are no objects a priori to activity. I refer to Roth (2011) to support this difference, he notes that “Kant, Piaget, the constructivists, and the embodiment/enactivist theorists all presuppose a subject…” (p. 225). Ingold’s provocation goes one step further than Roth’s observation by denying any a priori distinctions of individuated entities. This has profound implications for what mathematics is since it cannot be found “in” the cognizing subject. This is the second deviation. Mathematical concepts are framed as material. In the following section, I describe three different theoretical approaches that challenge the positioning of humans in activity and also in their conceptualizing of tools and of concepts.
In this section, I look at Andrew Pickering, who draws attention to the temporal aspect of practice and gives materials a voice. I also look at Tim Ingold, an anthropologist who proposes that all “things” are snapshots of processes, including tools. I also draw on Barad for her approach to concepts as physical apparatus. Finally, I move to de Freitas and Sinclair’s elaboration of Barad’s materialism in a mathematics educational framework. These perspectives each contribute a certain way of looking at data, and I suggest they lead to pressing questions and insights that support a unique way of seeing mathematics emerge from tool use.
Pickering (1995) offers the most accessible approach to the interactions of tool and human arguing for a back and forth model. He is concerned with the advancement and progression of scientific practice (including mathematics) in activity. In one of his case studies, he articulates how Donald Glaser attempts to accumulate data on strange particles. Pickering argues that in Glaser’s experimentation obstacles were a natural part of interacting with materials. Consequently, Glaser’s final result was very different from his initial intentions.
Pickering uses this example to emphasize that materials influence our activities. Thus, Pickering presents an analysis of scientific advancement in action in which material agency, as he calls it, is attributed to the natural phenomena with which scientists interact. His model can be summed up simply: materials can be understood as having agency when their structures, make-up and design restrict the subject within a context of activity. Pickering then argues that scientists will accommodate their actions to overcome obstacles, and identifies accommodation as a response to these obstacles. In this way accommodation can be seen as a readjustment of action.
I suggest that material agency has its relevance in mathematics specifically when working with tools. I draw on Pickering’s constructs of resistance and accommodation as a way of approaching the phenomenon of an individual interacting with a material, specifically, material tools. For Pickering, the construct of resistance can be seen as an obstacle to performing an action. On the other hand, accommodation is the response to resistance, usually in the form of a readjustment of an act. Pickering’s construct of resistance is the important construct and may need some elaboration. For Pickering, the construct of resistance can be seen as an obstacle to performing an action. It is important to understand in his model that resistance is not a human action but a material action. That is, resistance is a material obstruction to a goal or an intention. But resistance, according to Pickering, goes beyond the simple notion of impeding, it is for him both a micro and a macro construct in that it is not only a “challenge” to overcome but also a way that materials, those outside the bounds of social norms and subjective interpretation, determine action. Resistance, for example, can be thought of as a “voice” of an entity—a voice that is not audible but is expressed as a dynamic, in the moment, emergence of form. In this way, resistance can be thought of as an expression of the material's agency, giving it a dynamic, active “voice”. Given that accommodation, or readjustment, on the part of the human depends upon the resistance of the material, and drives the activity in a fundamental way, it highlights that movement does not reside solely in human initiation.
Although a quick interpretation of this model seems to support a binary divide between the human and the tool, as well as centralizing the construct of accommodation in the human, this reading does not necessarily commit us to an anthropocentric point of view. In fact, one of the goals of Pickering is to move away from human centric activity and he does this by offering the construct of material agency. His model is not about expressing a truth statement (Lyotard, 1984) of what is occurring, it is rather a shift of attention that can help illuminate different ways of seeing.
The importance of activity and interaction identified in the previous section, leads me to identify a process ontology as a significant part in developing theoretical frames in approaching mathematical activity. I draw from Alfred North Whitehead (1929/1978) who privileges process as the ontological realty of the world. For any entity to be identified, it is important to consider that there was a preceding activity that brought it to its current “state”. Ingold (2011) extends Whitehead by describing all “things” as processes, and while “being” implies a state, “becoming” is a process. Humans become as they unfold within the weave of the world. He writes, “to move, to know, and to describe are not separate operations that follow one another in series, but rather parallel facets of the same process” (p. xii) implicating not only the practices of a researcher but also the process of learning. In movement then, a person elicits a knowing which is not a “property of knowing” but a “practice of knowing” and where “knowledge is perpetually under construction within the field of relations" (p. 159) in particular material contexts.
Ingold also values the material experience before the mental act. In the western world, epistemology is seen in terms of ideas and images, but for Ingold, meanings of things come from our embodied experience. Ingold states, “practical activity brings incorporeal minds into contact with a material world” (p. 21) and such a process defines the actors. The person is seen as a manifestation of a process of becoming, of continuous creation. This process ontology moves us from a noun-oriented understanding of things to a more verb-oriented approach where all “things” are always in motion. The significance of tools is not in their distinct demarcation, but rather in the role these features play—their dynamism—in relations with human actors. In this study’s analysis, I will mobilize the notion that meaning emerges only in relations.
For Ingold, the metaphor of lines is very valuable for distinguishing the process of becoming from the state of being. He contrasts the notion of direct lines, which imply transport or a passage from one place to another, with that of wayfaring, which can be thought of as improvisational movement that carves out a path from a starting point. While direct lines require the implementation of intentions, mental images or models in order to get from one place to another (for example, from one van Hiele level to the next), wayfaring is first and foremost about the going or the moving. Ingold uses the example of looking at art in a gallery to illuminate the difference between direct lines and wayfaring by arguing that looking at art is not a “shuttling back and forth between radically opposed and mutually exclusive domains of mind and world […] but rather to bind mind and world in an ongoing movement” (p. 178). As can be seen in this quotation, Ingold is trying to reinscribe thinking within the temporal world of lived experience where there are no station stops to mark new thoughts. If we take looking at art, in Ingold’s description, to be like using mathematics tools, then we can see the latter as being less about the development of mental schemes or intentional, efficient deployment, and more about a fused, mind-world movement. In this framing, it becomes important to attend to the largely spontaneous movements of the wayfarer. This can be hard to do in post-hoc assessments of what has changed during mathematical activity, when the direct lines metaphor encourages a view of there having been transport from state A to state B.
It is within this framework that Ingold (2011) presents a perspective that does not see “things” but adopts emergence in activity as a way of “seeing” reality. That is, he argues one makes a conscious choice to bypass an a priori reflection and offers the notion of narrative to describe the process of movement and knowing. It may seem common sense to identify objects when we look at the world, identifying this and that as objects ready-to-use or as things that exist. However, if we are to take seriously a process ontology, identifying objects can misinform. Things “exist” and are “present” if we choose to draw a boundary around them and speak and/or think of them differently than the “other things” around it, but this, of course, is less an ontological reality than it is a choice of distinction or classification.
According to linguist, Deutscher (2010), language affects how one thinks and perceives the world. The act of nominalization that is common in represetationalist theories of mind can affect how one sees. English is a noun-based language and its use can suggest that it is things or beings that act. Ingold’s metaphor is important in this regard because the line does not connect the subject and object like it might do in Pickering’s framing or in Actor Network Theory (Latour, 1987). Instead the line travels in a wavy pattern back and forth between the “subject” and “object” but the line only moves toward or away. The purpose of this metaphor is that it helps shift attention away from the objects so that theorizing of individual things are curtailed because according to a non-dualist ontology nothing acts alone. It is not just an attempt to break down the ontological divide between being and things but also to shift our gaze of analysis to one of function. Ingold elaborates his argument against identifying objects as things in and of themselves by suggesting that tools are not determined by their names but by their “storied past”. He uses his own experience of sawing wood as an example to illustrate how the saw as well as himself are drawn into use and become tool and sawer together in activity. He argues that it is not an example of a human using an appropriated tool. The functionality of a tool, if one can describe it as such, is not a result its form or its design alone but is based on its history of use. A distinguishing aspect of Ingold’s articulation of tool as narrative is his moving away from an outline of form. An outline, for Ingold, is to make a distinction between inner and outer; it is to establish a boundary and, for Ingold, this boundary is the delineation of a closure in which movement is restricted.
It is within all these considerations that Ingold challenges the notion of affordance originally put forth by Gibson. According to Ingold, Gibson’s notion of affordance is an elusive quality, one that Gibson has trouble reconciling. Gibson states, “But, actually, an affordance is neither an objective property nor a subjective property; or it is both if you like.” (in Ingold, 2011). Ingold notes that Gibson cannot quite commit to whether an affordance exists in the object or in the relation of use. Ingold troubles the notion of affordance arguing that an affordance cannot exist prior to activity. If, for example, a child is placed in a room with a bunch of toys, one might argue that they will see toys and play with them but this only shows that a child can listen to instruction and imitate an approach to a world that has already been organized by way of language and interaction. For Ingold, these toys would not be toys until they are “toyed” with, and only then the playing and the engagement that emerges is what “possibly” makes them toys, not because they are called toys in the first place. Meta-level descriptions of students working with tools may seem similar in certain ways. For example, the students drew a circle with a compass. However, in more nuanced and detailed observation the narratives of each student might be quite different: some students had their compass slip, one drew an ellipse, another drew part of the circle off their paper. But even in these examples, there are problems because if we accept the notion that there are no things preceding activity, we should not begin the narrative with a student nor a compass. We should begin with a narrative of movement. This approach engages descriptions that do not define a trajectory-like approach to an outcome (eg. drawing a circle) but engages us in a description of a wayfarer, one who becomes and does in the moment, where an endpoint is not conceived (partly because there is no endpoint).
In this section I go further with relations in activity and challenge the boundaries of things. Barad (2007), a philosopher, feminist and physicist, adopts a post-humanist perspective in analyzing Neils Bohr’s quantum physics theories emerging out of early 20th century. She seeks to address Bohr’s philosophy that concepts depend upon arrangement of apparatus. Bohr’s contemplations of the two-slit experiment and the resulting wave-particle duality of light motivates Barad. She notes while much of the community debated the nature of light, Bohr observed that it was the “actual experiments that displayed the “dual” nature of matter and light” (p. 105). By looking at this example, Barad concludes “the nature of observed phenomenon changes with corresponding changes in apparatus” (p. 106). Concepts are not ideational, they depend upon physical apparatus. Apparatus is not something that sits on a shelf waiting to serve a particular purpose, Barad argues that science experiments have shown throughout history that apparatus are constituted through practice and are often rearticulated in new reworkings; thus, the apparatus is usually thought to merely aid in identifying the concept but is more appropriately thought of as creating them. Similar to Ingold, Barad argues apparatus does not “pre-exist the experiment but rather emerges from it” (p. 142).
Barad aligning with Ingold argues “objects are not already there; they emerge through specific practices” (p. 157). To move away from object and subject, Barad uses the term intra-action as an alternative to interaction, positing that the prefix “intra-” is more ontologically sound than “inter-” given that things do not come to act together as individual, fixed parts but rather become together depending on their relation. Building upon Barad’s work, de Freitas and Sinclair (2014) describe the inseparability of concept and matter. They argue that the performative boundary making in activity animates the mathematical. This perspective is much more temporal and fluid, challenging the traditional approach of “acquiring” mathematical ideas. Instead, mathematics becomes more an experience than reflection. de Freitas and Sinclair, drawing from Barad and extending to mathematics via the work of the philosopher of mathematics Gilles Châtelet (2000), term their approach “inclusive materialism” indicating that their “theory of matter [...] resists the binary divide between human agency and inert passive matter” (p. 39). Revitalizing materials often considered to be passive or inert challenges the idea of concepts, animating them in terms of materiality. de Freitas and Sinclair theorize mathematics concepts as engaging both the logical and ontological and argue the fusing and couplings of speech, movement and material items including the body, is the mathematics. In this dynamic relation where mathematics is animated by material tools, practice is affected.
As an example, de Freitas and Sinclair (2014) draw on speech in a learning environment as an example of becoming in the moment. They argue that speech is not a medium to reflect what the thinker has already articulated in the mind, but instead organically flows in real time, as context, gestures and other factors are all active, changing and influencing. To ascribe speech a meaning of communication and/or representation relies too heavily on the meaning of words and to the intention of the speaker, but instead it should be seen as one of the many material factors that participate in a material assemblage of learning. These writers focus on activity, not as a process of acting based on what is already known, but as becoming and learning in movement.
The tool and student, together, and what they can do, together, is what can be referred to as coupling (de Freitas & Sinclair, 2014) or fusing (Barad, 2007). I refer to a hyphenated combination “student-tool” to specify this single entity. As such, the focus now is what the new entity can do as opposed to concern over what individuated objects bring to each other. Mathematics, tools and students become a single focus, with a singular agency of production. The inclusive materialism, outlined by de Freitas and Sinclair describe the practice of mathematics as a material engagement of student, movement, tool. The mathematical concept is the intra-action, a human subject with the tool. The concept, therefore, partakes of the physical world; the concept is material. Although a classroom can be seen as divided up discretely (ie. projectors, students), all movements, shifts, transformations are continuous and universes are being made known. There is neither origin nor final cause. There is only a weave of becoming.
To address a method of observing students intra-acting with a digital tool is challenging when both Ingold and Barad argue there are no things a priori to activity. It is important to adopt a more accessible way to engage in an analysis and I draw on Pickering who provides a methodology that identifies subject and object and offers an accessible way to engage in language about things. For example, one can identify resistance by looking for obstacles. Such a task is not easy from a non-anthropocentric point of view since obstacles are typically framed in relation to what the student is trying to do. Nonetheless, I suggest that it is always possible to counter the anthropocentric perspective by taking into consideration that the student must respond to the resistance—which is to say the material agency—of the tool. One can identify an obstacle by watching for sudden changes in action and attempting to decipher whether there was a significant reason for doing so. For example, if a student is using a compass and the graphite piece breaks, and the student subsequently stops using the compass, one can infer the breaking of the tool was an obstacle. To take another example, if in using a ruler to draw a line, the ruler slides slightly so that the angle of the line changes and the student stops drawing the line, then one can identify the sliding ruler as an obstacle. In these examples, the student is not able to perform an action—his or her motions or gestures are restricted. This noticing of obstacles offers a way of identifying the student’s active, in-the-moment experiences in mathematical practice. While Pickering’s model will be used as a way of engaging in observation the other theoretical lenses, materialism (drawing on Barad as well as de Freitas and Sinclair) and a process-ontology (drawing on Whitehead and Ingold) will be mobilized as well. A process approach attends to how particular aspects of students and the tool come together and their role in performing an action together. One can pair a process approach with a materialist view noting that it is important not to assign any aspect of movement or action to a hidden phenomenon such as thinking, but rather only to that which is observable. Process attends less to nouns and more to verbs; it is the relation and action between fused people-and-things that are the fundamental building blocks of reality (Whitehead, 1978).
Data collection for this study took place at a high school in Western Canada involving a grade nine class of approximately thirty students. The grade nine class was chosen because the mathematics curriculum for this grade includes a comprehensive geometric component where students work with rotational and line symmetries, reflections, polygons and circle geometry. The students had studied basic polygons and their properties in previous grades. Therefore, the pedagogical purpose of the activity was for the students to experience some common polygons as a form of review and renewal. The episode outlined in this paper occurred in a computer lab that the students had not visited before and where students were introduced for the first time to The Geometer’s Sketchpad (GSP) (Jackiw, 2001). They were requested to construct a triangle and a square using GSP.
Consider the following two episodes:
Two grade nine students, Calvin and Jonas, constructed a triangle by using the segment tool and also by constructing an interior. They then dragged the triangle all over the screen and when the triangle was half off the screen, one of the boys posed the question, “Is this a triangle?” Before addressing this interesting question, I will first look at the process of movement involving the body, the tool and the triangle and subsequently identify resistance within that movement.

Figure 1. Calvin’s triangle being translated around the screen
Figures 1 a, b, and c, are snapshots from a mathematical activity, in which Calvin moved the triangle around the screen employing different motions, in different directions and at different speeds. These images, when seen as static hide the previous activity as well as in-between and future movements. In terms of their temporal existence, it might seem like they are static representations of the tool’s affordance; that the student was the agent and the tool passively allowed the student’s predetermined actions.
If movement occurs before thought, as Ingold insists, then the hand-action that glides the mouse across the desk, while consequently dragging the triangle’s vertex on the screen, fuses human and tool (hand and mouse) in a continuous flow. This flow of movement saw the triangle move upward, downward, to the left, and line up with the edge of the screen. Human-centric theorists might describe this event in terms of Calvin’s use of a “random” or “wandering” drag mode (Arzarello et al., 2002), but this ascribes all the agency and intention to Calvin (who may be wanting to see simply what happens or does not know what else to do). In contrast, through a movement lens, the mind is not observing and leading, it is participating, in parallel with the tools (and the size, as well as friction, of the desk). The movements translate the knowing and learning; the knowing is the translated triangle. After a short period of time, the movement translated into the question “Is this a triangle?”
To describe the question as separate from the boy’s activity is to miss the process of his movements as well as create a binary divide between thought and action. It theorizes a dual role for the student—one as the mover and the other as the observer—but only one role for the tool: allowing the student to act upon and question it. Ingold (2011) reminds us that moving and knowing are the same process; similarly, Roth and Radford (2011) insist that thinking is not externalized but becomes. It is a challenge to shift from a paradigm that sees the student dragging the shape around the screen and attributing the intention, “Oh I can drag the triangle off the screen”, to a paradigm that sees the thinking in the hand-mouse gesture. While Calvin is limited in perception by the material tools, including a bordered screen, and in movement, by the shape of his hand and the desk, he nonetheless “feels” the ability of “hiding”, “cutting”, and “dragging off” part of the triangle. Doing justice to the movement of a wayfarer requires honouring it as it unfolds, rather than seeing it as a path of transport towards pre-determined ends or as a result of a conscious, deliberate decision.
In this episode, the movement seems to give rise to a kind of resistance, or an obstacle, which does not appear until the translating motion of the shape is limited by the edge of the screen. In other words, the edge of the screen only becomes interesting under motion, without it, it may not ever be noticed. When its boundary is approached, reached and then transgressed, it begins to intra-act with the moving hand-mouse, and becomes a participant in occasioning new activity. In this case, the transgression gives rise to a triangle that seems visually truncated at the end of the dragging, while retaining an integrity in time that warrants the name “triangle”. The question, “Is this a triangle?” highlights an accommodation-like action. The resistance of the edge of the screen, which “hides” part of the triangle, and the question that emerges becomes part of a story, part of an action.
A truncated triangle drawn on a whiteboard would probably not be considered a triangle, especially if the action of the drawing and/or gesturing hand, which may be extending off the edge is ignored. However, in the gesture-triangle-edge intra-action that produces the shape that used to be a triangle, the resistance cannot just be seen as being imposed by the edge of the screen, but also in the question itself. Indeed, if it was a triangle, it should still be a triangle, and it would also be a triangle if the edge of the window were enlarged. And surely the gesturing hand is still holding the invisible vertex in place, even when moving it around so as to affect the visible sides of the triangle?
Students were asked to make a square but often their shape did not hold under dragging, the students tried other methods to create more robust squares. What emerged from this process is what I term an almost-square (Figure 2). They may well have looked liked squares before, but the visible measurements exposed the second decimal place difference in the unequal lengths.
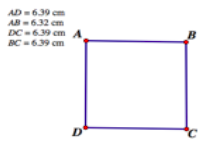
Figure 2. An almost-square
Before using the measure tool, the dragging hand was entangled with the watchful eye, as the quadrilateral changed on the screen. Instead of focusing on the student’s intention and the tool’s response, the notion of assemblage draws our attention to the relations among the tool, the student and the concept. Once the measuring tool comes into play, as well as the measurements lastingly being visible on the screen, the activity changed. The students began to drag the vertices of the square in order to adjust the measurements so that the side lengths would all match. But as soon as they dragged one vertex to match two sides, a third side would change in length and therefore no longer match the other sides. In response to this, a certain student pair then dragged the vertex associated with the distorted side ever so slightly, in an attempt to make all four sides match, only to find in movement that once again this led to a different kind of disfigurement. This back-and-forth dragging continued for a while. Now the almost-square emerged out of the actions of the dragging hand, which changed the measurements on the screen, which provoke further dragging. The relation changed as the segments themselves faded away to give primacy to the numbers, which now dictate the extent to which the shape could be considered a square.
The measuring became part of (and set in motion) an activity of adjustment, which can be seen as an accommodation that gave rise to a new assemblage. The resistance manifests itself through the unequal measurements, which nonetheless have the potential to be made equal (or so it may seem), which are related to the known properties of the square. The dragging of the vertex to try to “fix” the almost-square can be seen as an accommodation made by the hand and prompted by the resistance encountered in movement. The properties gain new meanings in that the previous way in which the sides could merely look the same now gets replaced with them all having to be equal in measure, one to the other. It is crucial here to recognize that the dragging is not controlled by the student, but spurred on by the changing measurements. For it is only when the measurements indicate a need for change did the vertex get dragged. Accommodation in this episode is not simply overcoming the stubbornness of the tool in an intentional change of strategy; rather, it is about a changing assemblage in which new relations come to the fore, leaving previously central “actors” (like the segments) to recede while new ones (the measurements) emerge. Throughout, the hand, tool, eye are in motion, in continual reconfiguration. The on-going struggle for equilibrium is initiated and promoted by this assemblage of technology and student.
The process of how the almost-square came to be involves multiple steps. The software’s response, the movement of the hand–mouse, the pointing and the student’s readings of the measurements, all contribute to the movement from which the almost-square emerges. From a process perspective, the almost-square only exists in the activity of movement; it is dependent upon the intra-action with the student in terms of the initial construction and subsequent “adjustments” and “fine-tunings”. If left alone, it might merely be termed a quadrilateral, but in ongoing movement, it remains an almost-square. This is because in a process approach, we read it not from its shape at any particular point in time but through the process in which it is engaged—which, in this case, is asymptotically becoming a square. Therefore, within a process ontology, the almost-square does not exist as a noun, but as movement in a becoming state.
While Pickering’s constructs of resistance/accommodation are centered on the tool (which resists) and the user (who accommodates), my reading of the translation of the triangle showed that the resistance (the edge of the screen) can be seen as highlighting a certain relation—a Calvin–dragging relation that encounters an unexpected event that would not exist if each were taken in isolation. In other words, the resistance in this case was a result of activity between the student–tool and not the student alone, nor the tool alone.
In addition, the resistance was less about avoiding or overcoming a problem than it was about dwelling in the problem itself. As the triangle was dragged around the screen and eventually partly off the screen, the student–tool experience can be viewed as having provided an opportunity for the student–tool to experience something unexpected, which ended up flushing out a question—Is this a triangle?—that reconfigured the relations among the triangle, the dragging and Calvin. This prompts a question about when resistance might be seen as productive in a learning environment. The teacher could have insisted that the students restrict their dragging to the contours of the screen, in which case the boundary between triangle and not-triangle would have remained unchallenged. But this is the very boundary that the Lakatosian practice of concept formation through monster-adjusting and monster-barring seeks to identify and stress. Is the fact that a tool is involved in the process somehow less mathematical? Or might we come to see Calvin’s question as a legitimate one that perturbs boundaries imposed by the visible and the static in school geometry? In which case, accommodation is not to be seen as a singular response that fixes a transgression, but rather as a setting off of possibilities for engagement.
In contrast to episode 1, the resistance that was identified in the almost-square episode did not seem to be a result of the fused student–tool, but of fusing itself. That is, the resistance aligned more closely with Pickering’s model of a back-and-forth between the student and the tool. This leads to the question of whether there are different levels or layers of resistance. While in episode 1 intra-action seemed to be in the student–tool relation, the identification of resistance in this episode highlighted the back-and-forth between tool and student potentially supporting a perspective that distinguishes between the tool and student. So the question emerges of how to deal with resistance in this kind of example without assuming an a priori individuation of relata.
Perhaps the back-and-forth interpretation is not as relevant in the context of instant feedback where the measurements change as the dragging changes. If both are changing simultaneously, then the temporal ordering implied by a back-and-forth interpretation is misleading. It encourages a reading in which the student makes an intentional choice based on the outcome of the dragging, which reasserts the primacy of the student over the tool. The back-and-forth activity does not entail a metaphor of transport, but one of wayfaring. It is not that student is moving from an almost-square to a square as might be seen in a transport but that in movement, in the back and forthing, the almost-square emerges. But what might be gained from focusing on the relation rather than the relata? From a Baradian point of view, we are forced to reckon with the impossibility of separating the relata, which, in this case, encourages us to attend to the dragging/measuring process. This leads to different questions: instead of asking whether the student will ever succeed in making a square or whether the tool’s measurements will always prevent a square from happening, we ask what new meanings (about “square”) emerge?
Or, from an Ingoldian perspective, we ask what new narratives emerged. Indeed, Ingold helps with this relata-versus-relation tension by drawing on the construct of things-as-narrative. From this perspective, there is no student, nor is there a tool, before the back-and-forth activity. The student–tool is, in and of itself, a process according to Ingold. To identify movement within the student–tool entity is natural through an Ingoldian process lens.
The post-human starting point of this paper invites us to move away from the tendency to locate learning and thinking solely within the mind of the learner. Because of the tendency to place the learner at the centre of thinking and learning, and to look for changes in how the learner talks, acts and moves, it can be challenging to study mathematical learning situations from a post-humanist point of view. By drawing on some of the main constructs offered in the literature, such as resistance/accommodation, assemblage, intra-action, process and tools as narrative, none of which have been explicitly designed to account for educational research, I have attempted to find out what new insights such post-humanist constructs can provide and what new questions they prompt.
de Freitas & Sinclair (2014) attempt to mobilise the notion of assemblage by referring, for example, to the student-tool-concept as a whole. They also suggest ways both of attending to and of analysing data that re-materialise language and attempt to include broader material dimensions of activity, instead of simply attending to spoken words or to gestures—highlighting other sounds and rhythms that shape the ongoing activity.
The construct of resistance/accommodation was fruitful in identifying turning points in the two episodes, but also potentially invited a human-centric view in which the tool ends up being subordinate to the human. The constructs of intra-action and assemblage were then brought in as starting points for overcoming a human-centric perspective. These new constructs drew attention to the changing nature of relations and, in turn, to the evolving assemblages involved in each episode. However, it is challenging to describe mathematical learning in terms of assemblages. We may be able to see difference, but know very little about whether the difference is mathematically relevant.
The shift to the physical reconfigures what it means to do mathematics. As opposed to a theorizing of how the mind is learning, responding or interiorizing, this shift draws back to the “in-the-moment”, embodied experience of tooling, rather than using a tool—much as we talk about walking rather than using our legs. Considering the material and temporal experiences is to study mathematics education in a post-human and materialist way, but one, that as discussed, does have challenges. To think about mathematics in the classroom involving “tooling” rather than using tools, requires avoiding the tendency and tradition of isolating nouns, like “student”, “tool” and “concept” and locating meaning in their entanglement. This is particularly difficult when wishing to discuss particular aspects of an assemblage, as the tendency is then to detach that aspect or part from the whole. This approach demands that when discussing any part of an assemblage, the focus should be on the part’s role in the intra-activity, which is to say, how it acts as a verb and how it contributes to the assemblage’s movement.
A process ontology, the actions of student as wayfarer, and especially the notion of tool as narrative, draw attention to movement and temporality. Movement and temporality were vital in interpreting the exercise involving the triangle and the exercise involving the almost-square; the triangle and the almost-square would not have emerged—would not have meaning—if only the student or only the tool were considered as isolated and inert nouns. It was the doing—the fused nouns participating in the temporal verb of acting—that was the mathematical practice. To look at any single movement of transport from one static point to another, within the process of the student–tool assemblage changes the meaning entirely: one might miss the triangle entirely if, for example, it was only seen when it existed partly-off screen; one might only see a quadrilateral (noun) instead of the in-action almost-square. In analysing mathematical practice through a relational and verb-oriented process ontology, in seeing the student–tool as a line of becoming, the significance of the embodied experience and the material world are animated, consequentially changing the understanding of mathematics teaching and learning.
This study was motivated and mobilized by a reconfiguration of perspective that challenged presupposed objects and their subsequent interactions. This study did not specifically address the age old philosophical quandary of how material and mental combine but helped generate a shift to addressing how the fusing of student-tool reaches out into the larger classroom environment with questions like “Is this a triangle?” or “Is this a well-constructed square?” These questions emerge from a paradigm of intra-action and not solely a mental contemplation. I suggest there is significant difference in these two perspectives. In this study’s approach, mathematics is less a label for a specific type of practice than it is a name for a specific kind of coupling.
Artigue, M. (2002). Learning mathematics in CAS environment: the
genesis of a reflection about instrumentation and the dialectics
between technical and conceptual work. International Journal
of Computers For Mathematical Learning, 7:245-274.
Arzarello, F., Olivero, F., Paola, D., & Robutti, O. (2002). A
cognitive analysis of dragging practises in Cabri environments. Zentralblatt
für Didaktik der Mathematik, 34(3), 66-72.
Balacheff, N. (1988). Aspects of proof in pupils’ practice of
school mathematics. In D. Pimm (Ed.), Mathematics, teachers
and children. p. 216-235. London: Hodder & St.
Barad, Karen. (2007). Meeting the universe halfway: Quantum
physics and the entanglement of matter and meaning .
Durham, N.C.: Duke University Press.
Bartolini Bussi, M. G., & Mariotti, M. A. (2008). Semiotic
mediation in the mathematics classroom: artifacts and signs after
a Vygotskian perspective. In L. D. English (Ed.), Bussi, M. B.,
Jones, G. A., Lesh, R. A., Sriraman, B. (Assoc. Eds.), Handbook
of international research in mathematics education. New
York: Routledge.
Châtelet, G. (2000). Figuring space: Philosophy, mathematics
and physics. Dordrecht, The Netherlands: Kluwer.
de Freitas, E. & Sinclair, N. (2014). Mathematics and the
body: Material entanglements in the classroom. Cambridge
University Press.
Deutscher, G. (2010). Through the language glass: Why the
world looks different in other languages . Henry Holt and
Co. New York.
Dietiker, L. (2013). Mathematical texts as narrative: Rethinking
curriculum. For the Learning of Mathematics, 33(3),
14-19.
Goodchild, S. (2014). Enactivist theories. In S. Lerman (Ed.), Encyclopedia
of mathematics education. Heidelberg: Springer.
Hesse, M. (1980). Revolutions and reconstructions in the
philosophy of science. Bloomington: Indiana University
Press.
Ingold, T. (2011). Being alive: Essays on movement, knowledge
and description. London: Routledge.
Latour, Bruno. (1987). Science in action: How to follow
scientists through society. Cambridge, MA: Harvard
University.
Jackiw, N. (2001). The Geometer’s Sketchpad. Emeryville,
CA: Key Curriculum Press.
Lyotard, Jean-François. (1984). The Postmodern Condition: A
Report on Knowledge. Trans. Geoff Bennington and Brian
Massumi. Minneapolis: University of Minnesota.
Nemirovsky, R., Kelton, M. L. & Rhodehamel, B. (2013). Playing
mathematical instruments: Emerging perceptuomotor integration with
an interactive mathematics exhibit. Journal for Research in
Mathematics Education, 44(2), 372–415.
Pickering, A. (1995). The Mangle of Practice: Time, agency,
and science. Chicago: The university of Chicago Press.
Roth, Wolff-Michael. (2011). Passibility: At the limits of
the constructivist metaphor. Springer, Netherlands.
Roth. W-M., & Radford, L. (2011). A cultural historical
perspective on mathematics teaching and learning . Sense
publishers.
Rotman, B. (2008). Becoming beside ourselves: the alphabet,
ghosts, and distributed human being . Duke University
Press, London.
Ruthven, K. (2002). Instrumenting mathematical activity:
reflections on key studies of the educational use of computer
algebra systems. International Journal of Computers For
Mathematical Learning, 7:275-291.
Varela, F.J. & Thompson, E. & Rosch, E. (1991). The
embodied mind: Cognitive science and human experience
(First MIT Press paperback edition, 1993) Cambridge,
Massachusetts, London, England: The MIT Press.
Verillon, P. & Rabardel, P. (1995). Cognition and artifacts: a
contribution to the study of thought in relation to instrumented
activity. European Journal of Psychology in Education,
9(3): 77-101.
Waltz, S. (2006). Nonhumans unbound: Actor-Network theory and the
reconsideration of “things”. In educational foundations,
Summer-Fall.
Whitehead, A. N. (1978). Process and reality. New York:
The Free Press.